Section 3: Martingale and Anti-Martingale
There are basically two fundamental approaches in which most money management techniques fit in: Martingale and Anti-martingale.
Martingale
This approach states that as the account balance of the trading account decreases, the size of the trade should increase. This is a popular MM technique between gamblers. The basic principle of this approach is that as the account suffers losses, its ability to recover increases.
Take for instance a coin flip. After three consecutive tails, there is a good possibility that the next outcome will be heads (although each outcome is statistically independent from each other). A gambler then would bet $100 on heads for the next outcome. If it comes out tails, then the next bet would be $200 for heads again. And the gambler continues to double the bet size until the outcome is heads.
One of the main drawbacks of this approach is that it does not consider that each try is totally independent from each other. In other words, every try has a 50% probability to come out heads, regardless of how many tails or heads came out before.
Another drawback (applies directly to traders) is that money is not infinite. Over a 100 trials in a coin flip, there is a slim probability to have a row of 11 consecutive tails. If the gambler were to bet going for heads from the 3rd trial on doubling each try, the last bet would be $25,600 (starting at $100).
It would not be long before our money, and our nerve ran out.

The same goes for the trading environment. Imagine a trader that has an account of $100,000. He would start risking $1,000 on his first trade and doubling up on each following trade.
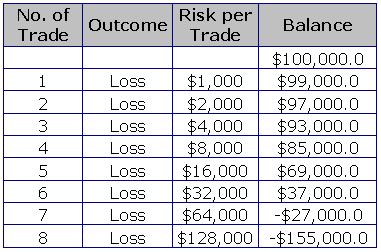
After the sixth consecutive loss, his trading balance would be at $37,000 and would need to risk $64,000 on his or her next trade. To do this, additional funds are required.
Anti-martingale
As you may have picked up from the name, this approach is exactly the opposite to the martingale approach. This one states that as the account increases in value, the amount risked should also increase, and when the account decreases in value, the trade size should decrease. The basic principle of this approach is that it permits the geometric growth of the account during strings of consecutive winning trades, and at the same time, it limits the losses during a drawdown period.
This approach makes more sense. When you are feeling more confident during a positive run, you trade more aggressively, and during drawdown’s, when you are less confident the size of your trades also decreases.
From this point on, we will only consider the anti-martingale approach.
The only drawback of this approach is that it suffers from what is called asymmetrical leverage. This means that during a drawdown period, the ability to recover losses decreases.
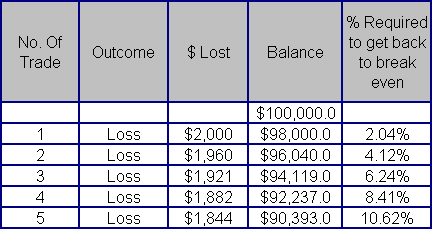
Imagine a trading account starting at $10,000. If we risk say 2% on each trade, after 5 consecutive losses our account would be at $9039.21 (a loss of 9.60% of the account.) However, to get back to break even we will need an increase of 10.63% of the new account level.
We hope we have convinced you that using proper money management techniques will increase your probability of success.
The following MM techniques fall into the anti-martingale approach and we will go into more detail on each in the following sections:
There are basically two fundamental approaches in which most money management techniques fit in: Martingale and Anti-martingale.
Martingale
This approach states that as the account balance of the trading account decreases, the size of the trade should increase. This is a popular MM technique between gamblers. The basic principle of this approach is that as the account suffers losses, its ability to recover increases.
Take for instance a coin flip. After three consecutive tails, there is a good possibility that the next outcome will be heads (although each outcome is statistically independent from each other). A gambler then would bet $100 on heads for the next outcome. If it comes out tails, then the next bet would be $200 for heads again. And the gambler continues to double the bet size until the outcome is heads.
One of the main drawbacks of this approach is that it does not consider that each try is totally independent from each other. In other words, every try has a 50% probability to come out heads, regardless of how many tails or heads came out before.
Another drawback (applies directly to traders) is that money is not infinite. Over a 100 trials in a coin flip, there is a slim probability to have a row of 11 consecutive tails. If the gambler were to bet going for heads from the 3rd trial on doubling each try, the last bet would be $25,600 (starting at $100).
It would not be long before our money, and our nerve ran out.

[Table 1]
The same goes for the trading environment. Imagine a trader that has an account of $100,000. He would start risking $1,000 on his first trade and doubling up on each following trade.

[Table 2]
After the sixth consecutive loss, his trading balance would be at $37,000 and would need to risk $64,000 on his or her next trade. To do this, additional funds are required.
Anti-martingale
As you may have picked up from the name, this approach is exactly the opposite to the martingale approach. This one states that as the account increases in value, the amount risked should also increase, and when the account decreases in value, the trade size should decrease. The basic principle of this approach is that it permits the geometric growth of the account during strings of consecutive winning trades, and at the same time, it limits the losses during a drawdown period.
This approach makes more sense. When you are feeling more confident during a positive run, you trade more aggressively, and during drawdown’s, when you are less confident the size of your trades also decreases.
From this point on, we will only consider the anti-martingale approach.
The only drawback of this approach is that it suffers from what is called asymmetrical leverage. This means that during a drawdown period, the ability to recover losses decreases.
Imagine a trading account starting at $10,000. If we risk say 2% on each trade, after 5 consecutive losses our account would be at $9039.21 (a loss of 9.60% of the account.) However, to get back to break even we will need an increase of 10.63% of the new account level.

[Table 3]
We hope we have convinced you that using proper money management techniques will increase your probability of success.
The following MM techniques fall into the anti-martingale approach and we will go into more detail on each in the following sections:
- One contract for every $XXXXX
- Fixed Fractional
- Optimal and Secure f
- Fixed Ratio

Post a Comment Blogger Facebook